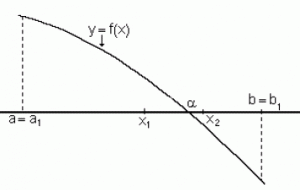
El método de bisección no es más que una sencilla fórmula matemática que permite que las variables sean despejadas lo más exactas posible para obtener el resultado deseado. En cortas palabras, es un algoritmo que permite la búsqueda de las raíces mediante las divisiones de sus intervalos y seleccionando los subintervalos que contengan.
Es decir, esta toma un intervalo que permita cerrar la raíz que se quiere resolver. Para lograr que se consiga esto, se agarra este mismo intervalo y se subdivide por la mitad, y de lo que se obtenga de referencia en la subdivisión, el producto que contenga la raíz se conserva, y se descarta la otra mitad (de esa misma subdivisión) que no la posea.
Para que se pueda resolver la ecuación en su totalidad, es preciso repetir todo este procedimiento para conseguir cuál es el valor en sí de la raíz que se está buscando. Y con ello se toma de punto de partida, el intervalo [a,b] que tiene que contener una raíz real y única de la función.
Características del método.
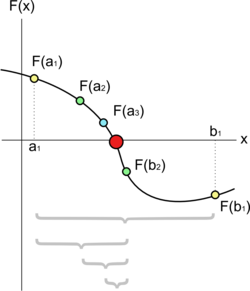Una de las características de este método, es que solo permite hallar una sola raíz, ya que su enfoque se basa en la tangencia de las x . Lo único que no es capaz el método de bisección, es demostrar diferencia entre la singularidad y su raíz.
Sus ventajas.
Lo beneficioso del método de Bisección es que tiene como prioridad determinar la cantidad de interacciones posibles para arrojar mínimos resultados con errores. Es decir, que los intervalos que se cierren en la raíz, tengan la menor valoración que de los que se obtienen de la épsilon.
En qué consiste.
El también conocido como método de intervalo medio, basándose en el teorema de valor intermedio, pauta que toda función continua f en un intervalo cerrado [a,c], sustrae todos los valores que se encuentran entre f (a) y f (b). Todo el valor que hay entre f (a) y f (b) es la imagen de uno de los intervalos de [a,b). En caso que las variables tengan signos opuestos, el valor 0 sería un intermedio entre f (j) y f (e), por lo que con total seguridad existe un p en [a,b] que cumple la siguiente forma f (p)=0. A través de esta forma, asegura el resultado de la ecuación como f (a)=0.
En pocas palabras, debe existir plena seguridad sobre la continuidad de la función f(x) en el intervalo [a,b]. Dependiendo de las condiciones, se puede obtener convergencias, además que arroja muy poca cantidad de error de redondeo.