 El método de Newton Raphson se le atribuye su nombre gracias al matemático inglés Joseph Raphson, del quien estuvo muy influenciado con los trabajos de su homólogo, Isaac Newton. Fue el autor del «Aequationum Universalis» y miembro de la Royal Society en 1961.
El método de Newton Raphson se le atribuye su nombre gracias al matemático inglés Joseph Raphson, del quien estuvo muy influenciado con los trabajos de su homólogo, Isaac Newton. Fue el autor del «Aequationum Universalis» y miembro de la Royal Society en 1961.
Este algoritmo matemático tiene como objetivo encontrar los acercamientos de los ceros o raíces de una función verdadera. Es por igual utilizada para encontrar el mínimo o máximo de una función, por lo que a consecuencia de esto, encuentra los ceros de su principal derivada.
Esta metodología que plantea Newton Raphson es de modo abierto, por lo que no garantiza en su totalidad la convergencia en sí. Y para lograr garantizar su convergencia, debe seleccionar un valor que esté lo más cercano posible a la raíz que se quiere buscar.
ÍNDICE
Todo dependerá de la raíz.
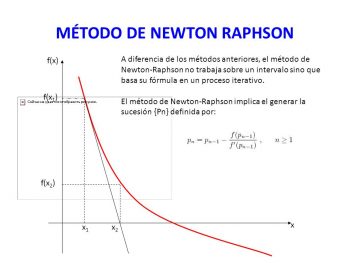
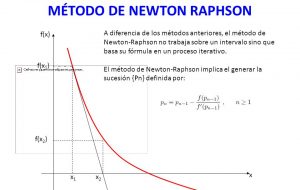
 De esta forma es como se comienza dicha búsqueda partiendo desde el valor más cercano al cero, quien será su punto de partida.
De esta forma es como se comienza dicha búsqueda partiendo desde el valor más cercano al cero, quien será su punto de partida.
Pero esto dependerá no solo de su ubicación, también si presenta múltiples puntos de inflexión que «giren» en torno a la raíz.
Esto hará que su divergencia aumente, lo cual es necesario elegir el valor predeterminado que está más cercano a la raíz.
Es un algoritmo lineal.
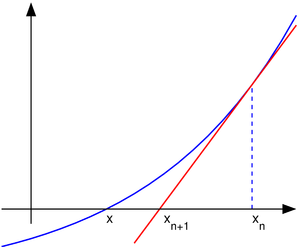
Una vez finalizado los últimos pasos, el método coloca en forma lineal la función por la recta tangente en el valor supuesto.
Las primeras dos coordenadas de origen de dicha recta, son las que permitirán un mejor acercamiento de la raíz que del valor anterior. Para que la convergencia funcione en su totalidad, deberá repetirse consecutivamente este procedimiento hasta dar con el blanco.
Cómo lograr la convergencia.
Uno de los factores a considerar en este método repetitivo, es que muchas veces sus resultados no logran obtener la convergencia.
Es por ello que si se quiere lograr, se requiere tener unos mejor conocimientos sobre las derivadas. En este caso ejemplar, si f’ (x) y f» (x) no se descartan y conservan el signo en [a,b] y f (x0) > 0, y la raíces del [a,b], el método logra convertir. De lo contrario, solo conseguirá su divergencia.
Formas de obtener el algoritmo.
Existen diversas formas para lograr la eficiencia del método de Newton Raphson, y las más usadas son por las que popularmente se les conoce.
La primera de ellas es mediante la interpretación geométrica, partiendo desde el método de la secante. Y la otra forma que se puede acudir es a través de un algoritmo donde se desarrolla la función f(x) en modo de serie de Taylor.