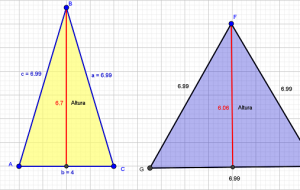
La altura de un triángulo es el segmento perpendicular a un lado que va desde el vértice opuesto a este lado (o a su prolongación). También puede entenderse como la distancia de un lado al vértice opuesto. Hay tres alturas (ha, hb y hc), según a qué lado está asociada dicha altura. A partir de la fórmula de Herón, conociendo los tres lados (a, b y c), se pueden hallar las tres alturas.
Las tres alturas del triángulo (o sus prolongaciones) se cortan en un punto llamado ortocentro. Las alturas podrían estar en el exterior del triángulo, en el caso de que sea un triángulo obtusángulo. El ortocentro también será exterior en los triángulos obtusángulos. En los rectángulos coincidirá con el vértice del ángulo recto. En los acutángulos, será un punto interior.
El extremo de la altura que está en la base o su prolongación, se denomina pie de la altura. La longitud de la altura, a menudo simplemente llamada «la altura», es la distancia entre la base extendida y el vértice. El proceso de dibujar la altura desde el vértice al pie se conoce como «bajar la altura» desde ese vértice. Es un caso especial de proyección.
La Altura de un Triángulo es
Ortocentro
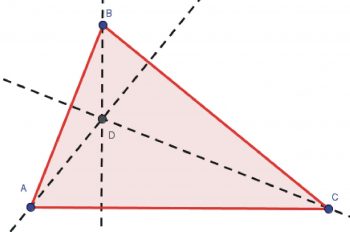Es el punto de intersección en el cual confluyen las tres altitudes de un triángulo. Es decir, en el ortocentro se cortan las tres alturas de un triángulo. Es simbolizado con la letra H mayúscula.
Cuando el triángulo es acutángulo, es decir, sus tres ángulos interiores son menores a 90°, el ortocentro será el incentro del triángulo órtico, aquel que presenta como vértices a los pies de las tres alturas. El incentro, simbolizado a partir de la letra I, que es el punto en el que se cortan las tres bisectrices de sus ángulos internos.
Si el triángulo es rectángulo, aquel que dispone de un ángulo recto de 90°, el ortocentro coincidirá con el vértice del ángulo recto. Y si el triángulo es obtusángulo, cuando uno de sus ángulos interiores es mayor a 90° y los otros dos miden menos de 90°, el ortocentro se ubicará por fuera del triángulo.
¿Cómo encontrar la altura de un triángulo?
Para calcular el área de un triángulo es necesario conocer su altura. Si no se tiene esta información, se puede calcular fácilmente tomando como base lo que se sabe.
- Paso 1: Usar la base y el área para hallar la altura
La fórmula para el área de un triángulo es A=1/2bh.
- A = área del triángulo
- b = longitud de la base del triángulo
- h = altura de la base del triángulo
- A= 1/2bh
- A=20
- b=4
- Paso 2: Mirar el triángulo y determinar las variables conocidas. En este caso, ya se conoce el área, así que se debe asignar ese valor a A. También se debe conocer el valor de la longitud de un lado, así hay que asignar ese valor a b. Si no se conoce el área ni la longitud de un lado, hay que intentar con otro método.
Cualquier lado de un triángulo puede ser la base, sin importar cómo esté dibujado el triángulo. Para visualizarlo, solo hay que imaginar que se rota el triángulo hasta que la longitud del lado conocida esté en la parte inferior.
Por ejemplo, si se sabe que el área de un triángulo es 20 y un lado es 4, entonces: A = 20 y b = 4.
Entonces: A= 1/2bh
- A=20
- b= 4
- 20 =1/2 (4) h
- 20=2h
- 10=h
- Paso 3: Insertar los valores a la ecuación A=1/2bh y hacer la operación.
Primero se debe multiplicar la base (b) por ½, luego dividir el área (A) por el producto. El valor que resulta será la altura del triángulo.
En el ejemplo: 20 = 1/2(4)h
- 20 = 2h
- 10 = h