 El triangulo se define como el polígono cerrado que posee tres lados. otras de las definiciones del triangulo es el polígono fundamental, debido a que todos los demás polígonos se pueden dividir en triángulos. también podemos definir que el triangulo es la figura formada por tres parte de recta en los que cada uno comparte los extremos con los otros dos.
El triangulo se define como el polígono cerrado que posee tres lados. otras de las definiciones del triangulo es el polígono fundamental, debido a que todos los demás polígonos se pueden dividir en triángulos. también podemos definir que el triangulo es la figura formada por tres parte de recta en los que cada uno comparte los extremos con los otros dos.
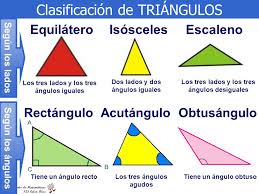
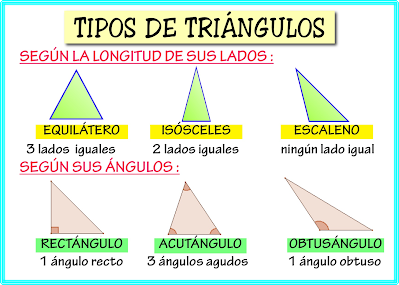
Los triángulos se pueden clasificar según sus lados donde se encuentran:
- El triangulo Equilátero: es que el posee todos sus lados de forma iguales.
- El triangulo llamado Isósceles: es el que tiene dos lados iguales y uno diferente.
- El triangulo Escaleno: es el triangulo que tiene todos sus lados diferentes.
ÍNDICE
Clasificación de los triángulos según sus ángulos
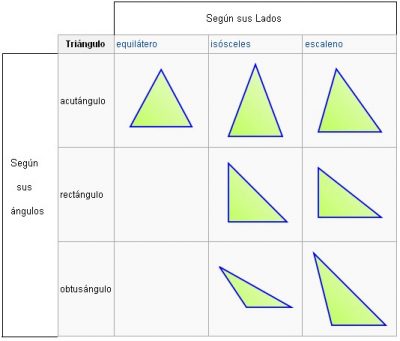 Los triángulos también se pueden clasificar según sus ángulos que son 3:
Los triángulos también se pueden clasificar según sus ángulos que son 3:
Acutángulos:
Se da cuando todos los ángulos de los triángulos son menores a 90 grados.
Rectángulos:
Si uno de los triángulos mide 90 grados, se verifica que ningún otro Angulo pueda llegar a medir 90 grados. En ese caso, se trata de un triangulo rectángulo. En un triangulo rectángulo, el lado opuesto al ángulo recto, de 90 grados, se llama hipotenusa. Los otros dos lados del triangulo rectángulo se llaman catetos.
Obtusángulos:
Si uno de los ángulos de un triangulo mide más de 90 grados, se verifica que ningún otro ángulo puede llegar a medir 90 grados. Un triangulo con un ángulo obtuso es un triangulo obtusángulo
Estructuras importantes comunes de los triángulos
Los triángulos cuentan con una estructura importante y común que son:
Alturas y Ortocentro:
Cada uno de los segmentos perpendiculares a los lados que parten de los ángulos en un triangulo recibe el nombre de altura. Se verifica que las tres alturas tienen un solo punto en común que recibe el nombre ortocentro
Mediatrices y Circuncentro:
Si se trazan las perpendiculares a los lados de un triangulo en su punto medio, se obtienen las mediatrices. Las mediatrices de un triangulo se encuentran en un punto que se denomina circuncentro. Ese punto coincide con el centro de la circunferencia que se circunscribe al triangulo.
Medianas y Baricentro:
Los segmentos que desde un vértice alcanza la mitad del lado opuesto se llaman medianas. Se puede demostrar que las medianas se cruzan en un punto que se denomina baricentro.
Bisectrices e Incentro:
Las bisectrices de un triangulo coinciden con las bisectrices de sus ángulos. También se puede demostrar que las tres bisectrices se cortan en un punto que se llama incentro. El incentro recibe ese nombre por coincidir con el centro de la circunferencia inscrita.
Criterios de igualdad de los triángulos
Existen tres criterios de igualdad o desigualdad de dos triángulos. En cualquier caso, nunca será necesario comprobar que los tres lados y los tres ángulos coincidan, basara con solo tomar tres medidas. Dados dos triángulos ABC y A.B.C, entonces son iguales si se cumple algunas de las tres condiciones:
- Igualdad de 2 lados y del ángulo que forman.
- Igualdad de 2 ángulos y del lado cuyos extremos son sus vértices.
- igualdad de los tres lados.
Cuando los triángulos son triángulos rectángulos, estas condiciones quedan simplificadas, ya que por ser rectángulos tienen un ángulo en común. Por ello, se puede dar los siguientes criterios de igualdad para los triángulos rectángulos:
- Igualdad de catetos.
- Igualdad de un cateto y uno los ángulos agudos.
- Igualdad de la hipotenusa y uno de los catetos.
- Que es el teorema de tales
Se dice que el teorema de tales es cuando el sistema de rectas paralelas corta dos rectas cualesquiera, los segmentos que se forman en una de ellas son respectivamente proporcionales a los segmentos correspondientes que se han formado con la otra