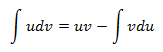Los métodos de integración son técnicas utilizadas para la resolución de ejercicios con integrales, usualmente necesarios para la medición de áreas y volúmenes en el espacio, por lo que es un concepto de extrema importancia en la ingeniería.
Las integrales no son más que las inversas de las derivadas. Para que todo concepto matemático exista, debe existir un contrario, como es bien conocido. Así, pues, las integrales son para las derivadas lo que la suma es a la resta o la división a la multiplicación.
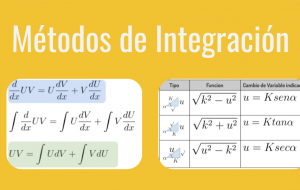
Dado el hecho de que las integrales pueden resultar complejas en la medida en que se hace más práctica y real su aplicación, es necesario el conocimiento de técnicas y procedimientos que simplifiquen y agilicen su resolución. Esto es lo que les presentaremos a continuación:
ÍNDICE
Cambio de Variable.
Se conoce por cambio de variable a la práctica de la sustitución de una incógnita por un término que la representa.
Esta es una de las técnicas más utilizadas gracias al grado de simplificación que ofrece, puesto que se pueden reducir expresiones enteras a un sólo término, cosa que agiliza de sobremanera la resolución de problemas y le permite ser utilizada para incrementar la eficiencia de otros métodos que veremos a continuación.
A la hora de realizar el cambio de variable, se recomienda envolver la mayor cantidad de elementos posibles, para evitar complicarse o necesitar sucesivos cambios.
Fracciones Parciales.
Se trata de la descomposición de un cociente con polinomios presente en una adición de fracciones con polinomios cuyo grado es menor. Para que se pueda utilizar esta técnica, el grado del denominador debe ser, necesariamente, mayor que el polinomio presente en el numerador.
Así, se pasa a expresar una fracción algebraica cualquiera con la forma de una suma de fracciones más pequeñas.
Identidades Trigonométricas.
Mediante la igualación de expresiones matemáticas a expresiones trigonométricas (véase el teorema de Pitágoras). Con esto, se puede adaptar una ecuación diferencial a una expresión más simple y rápida de solucionar mediante las identidades de seno, coseno, secante, entre otras.
Integración por Partes.
Se trata de separar una ecuación diferencial en donde el integrando se forma por un producto o multiplicación.
Se divide la ecuación (de dos factores) en uno “u” y otro “dv”. Se pasará a derivar “u” para obtener “du” e integrar “dv” para obtener “v” y aplicar la siguiente fórmula:
